#|
meteodaten <- read.csv('Data/meteodaten_saison.csv',
sep = ',',
header = TRUE)Appendix D — Übung 4: Deskriptive Statistik und Visualisierung
Arbeite mit den saisonalen Meteodaten, die wir im R-Kurs eingelesen haben
D.1 Histogramm und Kennzahlen
Ihr möchtet die mittlere Jahresniederschlagssumme und die mittlere Jahrestemperatur sowie deren Varianz von Jahr zu Jahr bestimmen, um die Klimabedingungen in Bern zu beschreiben.
Um die richtigen Kennzahlen (Mittelwert, Median, Modus, etc.) zu wählen, müssen wir die Verteilung der Daten kennen. Erstellt ein Histogramm der Jahresmitteltemperaturen und -niederschlag:
# Jahresdaten erstellen
# Berechne Jahresmittelwerte und -summen
jahresmitteltemp_bern <- aggregate(meteodaten$Bern_Mitteltemperatur ~ meteodaten$Jahr,
FUN = mean,
na.rm = TRUE)
jahresmitteltemp_grstbernhard <- aggregate(meteodaten$GrStBernhard_Mitteltemperatur ~ meteodaten$Jahr,
FUN = mean,
na.rm = TRUE)
jahresniederschlag_bern <- aggregate(meteodaten$Bern_Niederschlagssumme ~ meteodaten$Jahr,
FUN = sum,
na.rm = TRUE)
jahresniederschlag_grstbernhard <- aggregate(meteodaten$GrStBernhard_Niederschlagssumme ~ meteodaten$Jahr,
FUN = sum,
na.rm = TRUE)
# Kombiniere die Ergebnisse in eine neue Tabelle
jahresdaten <- data.frame(
Jahr = jahresmitteltemp_bern$`meteodaten$Jahr`,
Bern_Mitteltemperatur = jahresmitteltemp_bern$`meteodaten$Bern_Mitteltemperatur`,
GrStBernhard_Mitteltemperatur = jahresmitteltemp_grstbernhard$`meteodaten$GrStBernhard_Mitteltemperatur`,
Bern_Niederschlagssumme = jahresniederschlag_bern$`meteodaten$Bern_Niederschlagssumme`,
GrStBernhard_Niederschlagssumme = jahresniederschlag_grstbernhard$`meteodaten$GrStBernhard_Niederschlagssumme`
)
hist(jahresdaten$Bern_Mitteltemperatur,
main = 'Histogramm der Mitteltemperatur in Bern',
xlab = 'Mitteltemperatur (°C)',
ylab = 'Anzahl der Jahre',
xlim = c(6, 12),
ylim = c(0, 15),
breaks = 30)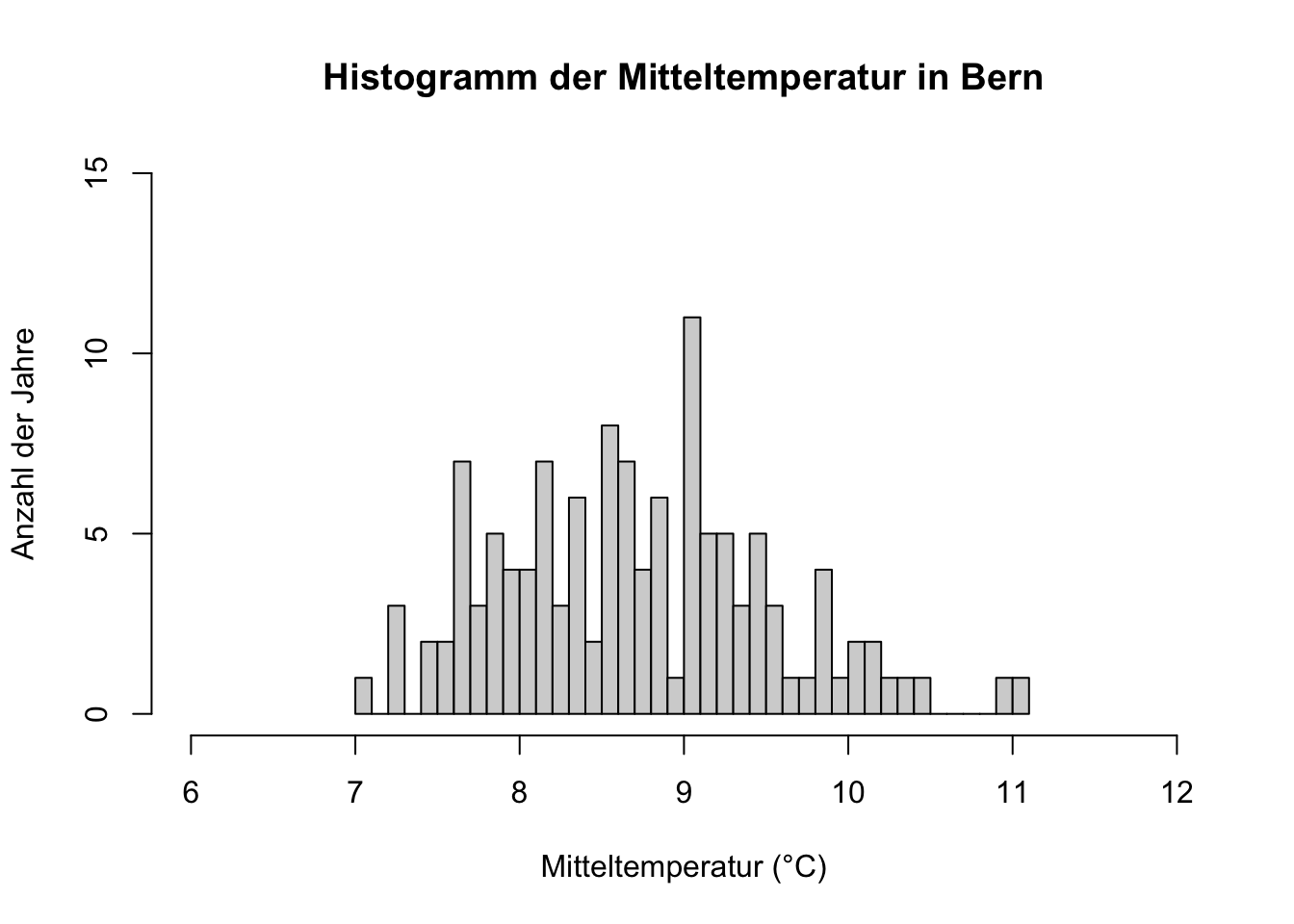
hist(jahresdaten$Bern_Niederschlagssumme,
main = 'Histogramm der Niederschlagssumme in Bern',
xlab = 'Niederschlagssumme (mm)',
ylab = 'Anzahl der Jahre',
xlim = c(500, 1500),
ylim = c(0, 10),
breaks = 30)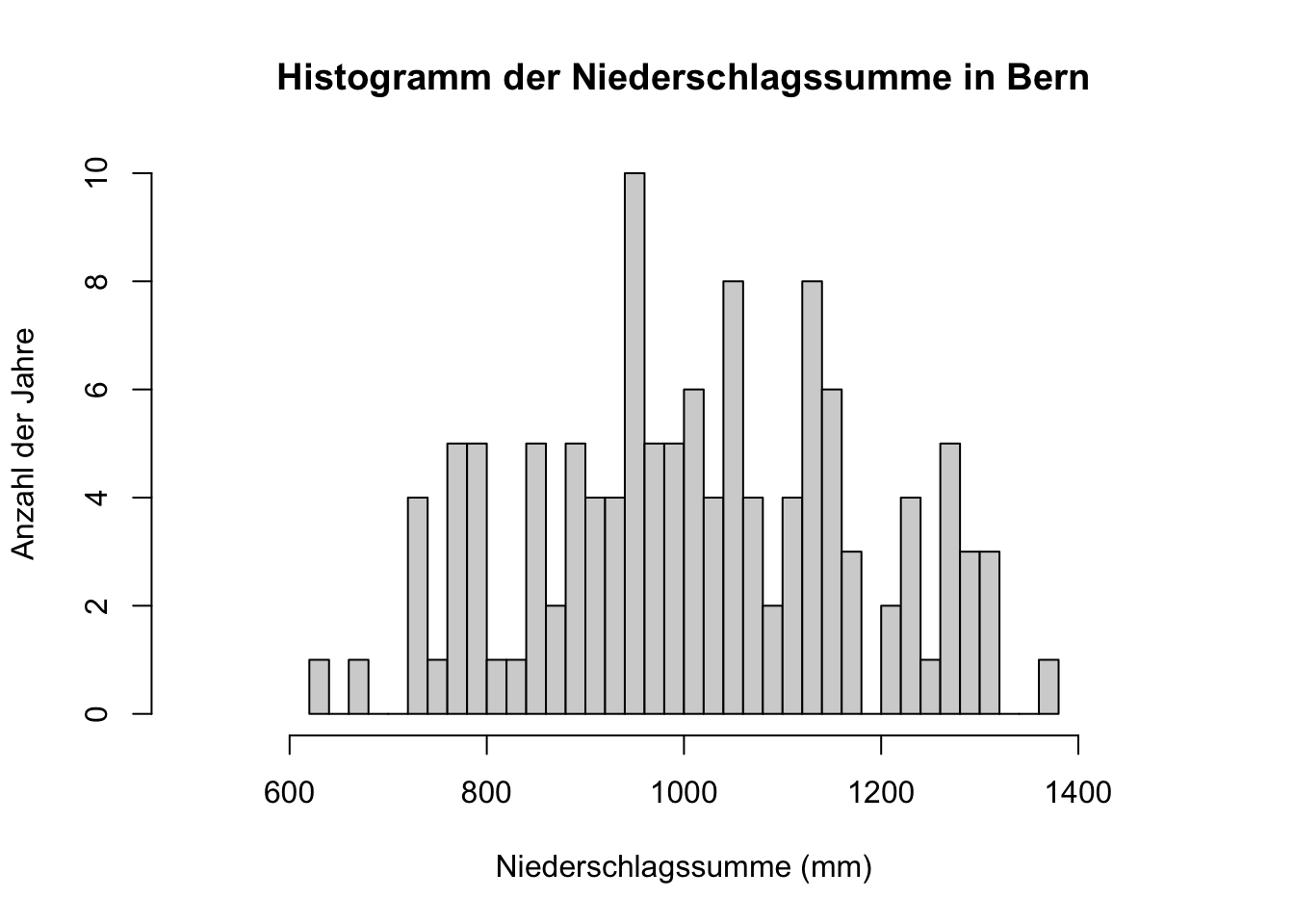
Beide Verteilungen sind ungefähr symmetrisch, da die Daten in der Mitte des Bereichs konzentriert sind und die Verteilung nach links und rechts ungefähr gleich ist. Dies ist aber mit so “wenigen” Daten nicht wirklich aussagekräftig. Das macht aber bei der Art der Daten Sinn, da die Temperatur und Niederschlagssumme in der Regel normalverteilt sind.
D.1.1 Kennzahlen
Welche Kennzahlen zur Beschreibung des Mittels und der Streuung kommen aufgrund den Verteilung und Skala der Daten in Frage?
Da die Daten normalverteilt sind, können wir den Mittelwert und die Standardabweichung verwenden, um die zentrale Tendenz und die Streuung der Daten zu beschreiben. Der Median ist auch eine gute Kennzahl, um die zentrale Tendenz zu beschreiben, da er robust gegenüber Ausreissern ist.
- Berechne Mittelwert, Median, Spannweite und Standardabweichung des jährlichen Temperaturen in Bern und schaue dir zusätzlich die Ausgabe der summary() Funktion von R an.
mean_temp_bern <- mean(jahresdaten$Bern_Mitteltemperatur)
print(mean_temp_bern)[1] 8.715176median_temp_bern <- median(jahresdaten$Bern_Mitteltemperatur)
print(median_temp_bern)[1] 8.666667range_temp_bern <- diff(range(jahresdaten$Bern_Mitteltemperatur))
range(jahresdaten$Bern_Mitteltemperatur)[1] 7.091667 11.050000print(range_temp_bern)[1] 3.958333sd_temp_bern <- sd(jahresdaten$Bern_Mitteltemperatur)
print(sd_temp_bern)[1] 0.8185026summary(jahresdaten$Bern_Mitteltemperatur) Min. 1st Qu. Median Mean 3rd Qu. Max.
7.092 8.104 8.667 8.715 9.221 11.050 Der Unterschied zwischen Mittelwert und Median (0.05°C) ist sehr klein, was darauf hindeutet, dass die Verteilung der Daten symmetrisch ist. Die Spannweite der Daten beträgt 3.96 °C, was darauf hindeutet, dass die Daten relativ eng um den Mittelwert verteilt sind. Die Standardabweichung beträgt 0.82°C, was darauf hindeutet, dass die Daten relativ homogen um den Mittelwert verteilt sind.
D.2 Kontingenztabelle
- Konvertiere die Spalte mit den Niederschlagssummen in Bern in Klassen, die jeweils 100 mm umfassen (Tipp: z.B. mit round() Funktion für Klassen: <50mm, 50-150mm, 150-250mm, …) Erstelle die Kontingenztabelle für die Anzahl der Regensummen in den 100 mm Klassen in den vier Jahreszeiten (table() Funktion)
0 100 200 300 400 500 600
Fruehling(MAM) ? ? ? ? ? ? ?
Herbst(SON) ? ? ? ? ? ? ?
Sommer(JJA) ? ? ? ? ? ? ?
Winter(DJF) ? ? ? ? ? ? ?Kontingenztabelle mit R erstellen
# 1. Erstelle Klassen für Niederschlagssummen in Bern in 100-mm-Schritten
# Die Spalte 'Saison' enthält die Jahreszeiten (z.B. 'Fruehling(MAM)', 'Sommer(JJA)')
# Die Spalte 'Bern_Niederschlagssumme' enthält die Niederschlagssummen
# Klassen für Niederschlagssummen in 100-mm-Schritten erstellen
meteodaten$Niederschlag_klassen <- cut(
meteodaten$Bern_Niederschlagssumme,
breaks = seq(0, max(meteodaten$Bern_Niederschlagssumme, na.rm = TRUE), by = 100),
include.lowest = TRUE,
right = FALSE
)Die Einteilung liesse sich auch einfacher machen, aber etwas weniger hübsch…
# Klassen für Niederschlagssummen in 100-mm-Schritten erstellen
meteodaten$Niederschlag_klassen <-
round(meteodaten$Bern_Niederschlagssumme/100)*100Wir arbeiten weiter mit der ersten Lösung.
# 2. Erstelle eine Kontingenztabelle
kontingenz_tabelle <- table(
meteodaten$Saison,
meteodaten$Niederschlag_klassen
)
# 3. Zeige die Kontingenztabelle an
print(kontingenz_tabelle)
[0,100) [100,200) [200,300) [300,400) [400,500) [500,600]
Fruehling(MAM) 0 36 60 25 1 1
Herbst(SON) 2 38 53 24 6 0
Sommer(JJA) 0 7 40 41 31 3
Winter(DJF) 14 59 45 5 0 0D.3 Visualisierung des Erwärmungstrends
- Visualisiert die Erwärmungstrend der Station Bern mit einem Liniendiagramm, indem du die Jahresmitteltemperatur darstellst und die 31-jährige Gleitende Mittel (auch “running mean” genannt z.B. mit der Funktion
runmean()aus der Bibliothek “caTools”) hinzufügst.
D.3.1 Liniendiagramm mit Gleitendem Mittel
# Bibliothek caTools laden
library(caTools)
# Berechnung des 31-jährigen gleitenden Mittels (Running Mean)
# Die Spalte für die Mitteltemperatur in Bern heisst 'Bern_Mitteltemperatur'
gleitendes_mittel <- runmean(jahresdaten$Bern_Mitteltemperatur, 31, align = "center", endrule = "mean")
# Liniendiagramm erstellen
plot(jahresdaten$Jahr, jahresdaten$Bern_Mitteltemperatur, type = "l", col = "blue",
xlab = "Jahr", ylab = "Mitteltemperatur in Bern (°C)",
main = "Erwärmungstrend der Station Bern mit 31-jährigem Gleitendem Mittel")
# Hinzufügen der Gleitenden Mittel-Linie (31-jähriges Running Mean)
lines(jahresdaten$Jahr, gleitendes_mittel, col = "red", lwd = 2)
# Legende hinzufügen
legend("topright", legend = c("Jahresmitteltemperatur", "31-jähriges Gleitendes Mittel"),
col = c("blue", "red"), lty = 1, lwd = 2)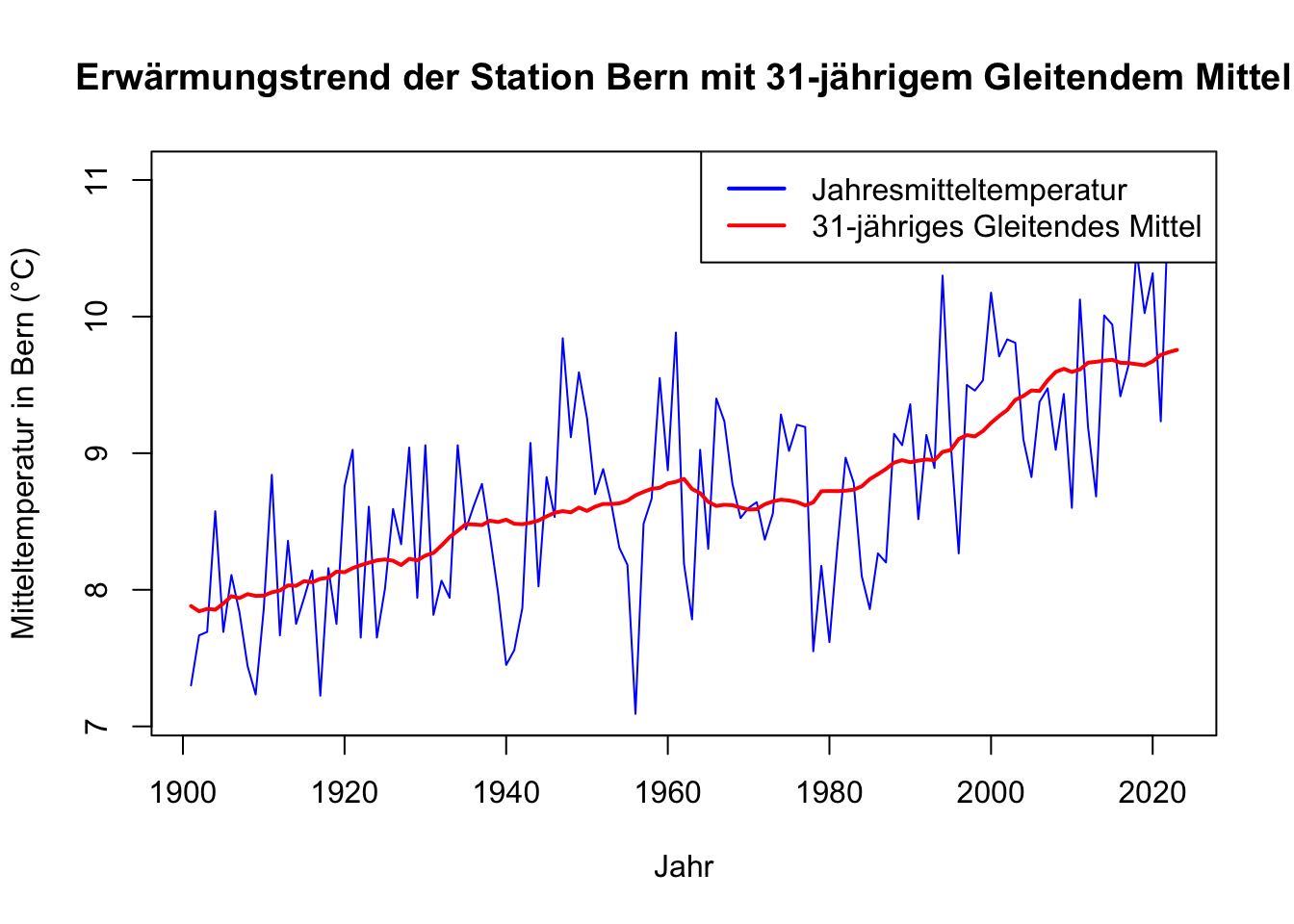
Erstelle zusätzlich zwei Abbildungen der Temperaturanomalien wie hier und hier:
D.3.2 Warming Stripes
# Bibliothek
# Bibliothek
library(ggplot2)
# Berechnung der Abweichung der Mitteltemperatur von der Referenzperiode 1961-1990
jahresdaten$Abweichung <- jahresdaten$Bern_Mitteltemperatur - mean(jahresdaten$Bern_Mitteltemperatur[jahresdaten$Jahr >= 1961 & jahresdaten$Jahr <= 1990])
# Erstelle die "Warming Stripes" mit Legende
ggplot(jahresdaten, aes(x = Jahr, y = 1, fill = Abweichung)) +
geom_tile() +
scale_fill_gradientn(
colours = c("blue", "lightblue", "white", "orange", "red", "darkred"),
name = "Temperaturabweichung (°C)"
) +
theme_void() + # Entfernt Achsen, Titel etc.
theme(legend.position = "bottom", legend.title = element_text(size = 10)) +
labs(title = "Schweizer Temperatur seit 1864")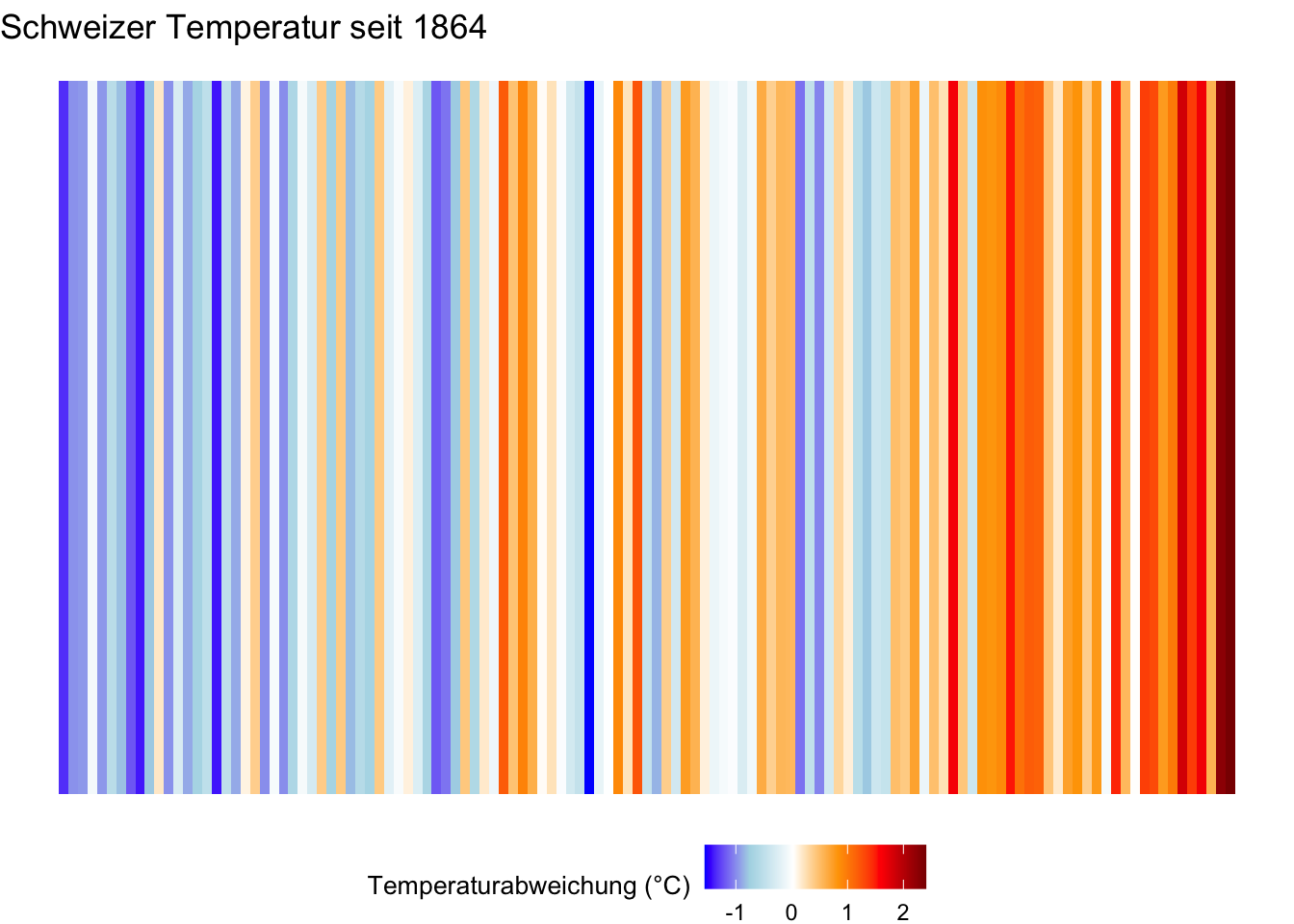
D.3.3 Barplot der Temperaturanomalien
# Bibliotheken
library(ggplot2)
# Erstelle einen Barplot, der die Abweichungen darstellt
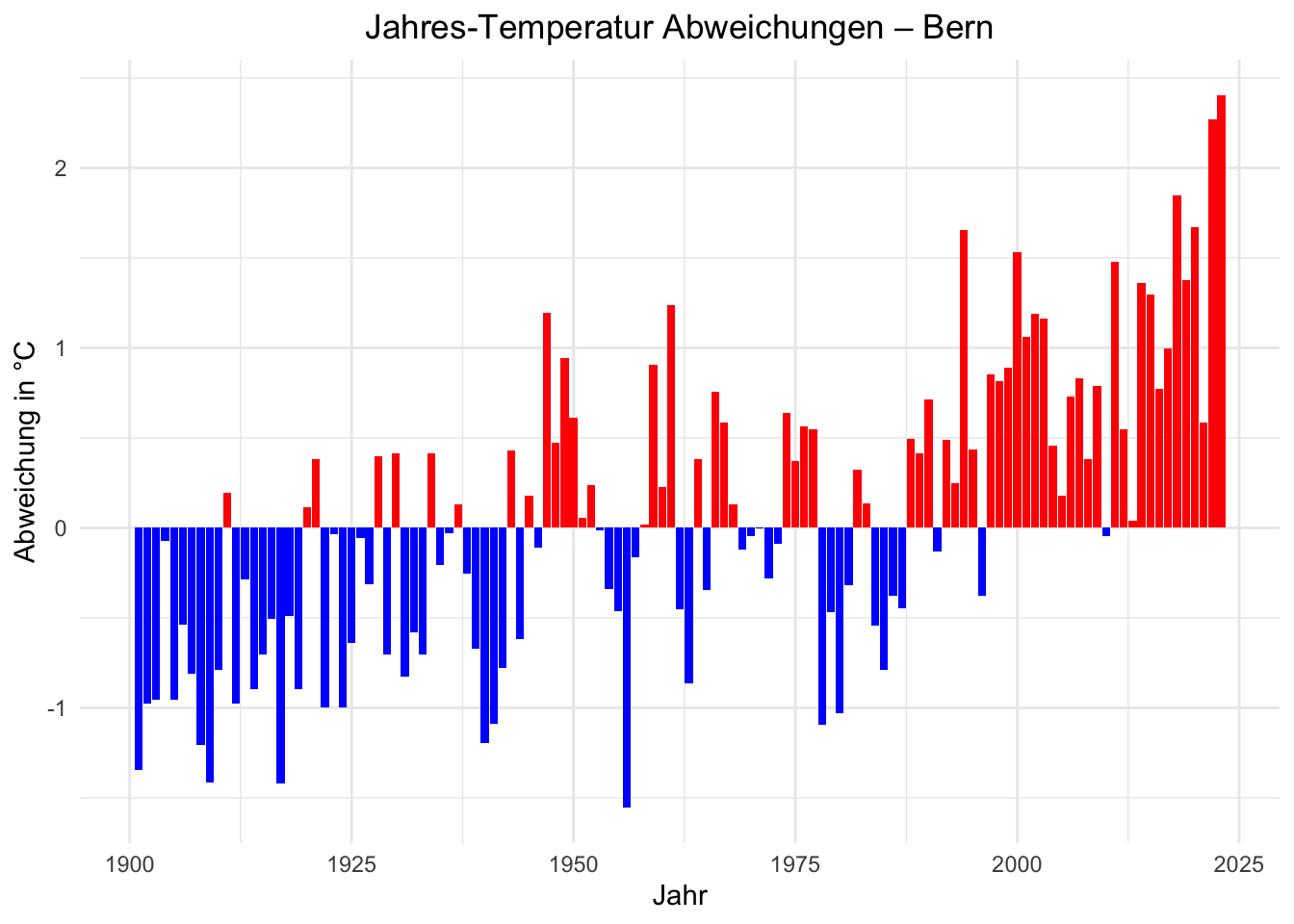
ggplot(jahresdaten, aes(x = Jahr, y = Abweichung, fill = Abweichung > 0)) +
geom_bar(stat = "identity", show.legend = FALSE) +
scale_fill_manual(values = c("blue", "red")) + # Farben: Blau für kälter, Rot für wärmer
theme_minimal() +
labs(title = "Jahres-Temperatur Abweichungen – Bern",
x = "Jahr",
y = "Abweichung in °C") +
theme(plot.title = element_text(hjust = 0.5)) # Zentriere den Titel