13  Hauptkomponentenanalyse

Die Hauptkomponentenanalyse (PCA) ist eine Methode der multivariaten Statistik, die zur Dimensionsreduktion von Datensätzen mit vielen Variablen eingesetzt wird. Ihr Ziel ist es, die Komplexität der Daten zu reduzieren, während möglichst viel der ursprünglichen Varianz erhalten bleibt. PCA wird in verschiedenen Bereichen wie der Datenanalyse, Mustererkennung und Visualisierung angewendet.

• Ziel ist eine Dimensionsreduktion, d.h. „Relevante“ Informationen mit einem Redundanz- und Rauschfilter zu extrahieren
• Es gibt viele redundante Informationen, z.B. weil Messungen benachbarter Stationen korreliert sind
• Die Daten enthalten nicht nur das Messsignal sondern auch Fehler

13.1 Grundidee

Die PCA transformiert die Ausgangsdaten in ein neues Koordinatensystem, in dem die grösste Varianz der Daten entlang der ersten Achse (der ersten Hauptkomponente) liegt. Die zweite Hauptkomponente erklärt die zweitgrösste Varianz und steht orthogonal zur ersten, und so weiter.

Wichtige Konzepte:

• Kovarianzmatrix: Beschreibt, wie stark zwei Variablen gemeinsam variieren.
• Eigenwerte und Eigenvektoren: Eigenwerte geben an, wie viel Varianz von einer Komponente erklärt wird; Eigenvektoren definieren die Richtung dieser Varianz.

13.2 Mathematische Herleitung

1. Standardisierung der Daten:

   • Um Variablen mit unterschiedlichen Einheiten vergleichbar zu machen, werden die Daten zentriert und skaliert.

2. Berechnung der Kovarianzmatrix: \[ \Sigma = \frac{1}{n-1} X^T X \]

3. Eigenwertzerlegung:

   • Lösung der Eigenwertgleichung: \[ \Sigma v = \lambda v \] wobei \(\lambda\) die Eigenwerte und \(v\) die Eigenvektoren sind.

4. Sortierung der Eigenwerte:

   • Die Eigenwerte werden in absteigender Reihenfolge sortiert, die zugehörigen Eigenvektoren bilden die Hauptkomponenten.

5. Transformation der Daten:

   • Projektion der Daten in den neuen Raum: \[ Z = XW \] wobei \(W\) die Matrix der Eigenvektoren ist.

13.3 Interpretation

• Erklärte Varianz: Der Anteil der Gesamtvarianz, der von jeder Hauptkomponente erklärt wird.
• Biplots: Visualisieren die Projektion der Daten und die Lasten der Variablen auf den Hauptkomponenten.

# Daten simulieren
set.seed(123)
data <- matrix(rnorm(100*5), ncol = 5)
colnames(data) <- paste0("Var", 1:5)

# PCA durchführen
pca_result <- prcomp(data, scale. = TRUE)

# Zusammenfassung
summary(pca_result)
# Scree-Plot
plot(pca_result, type = "l")

# Biplot
biplot(pca_result, scale = 0)

Importance of components:
                          PC1    PC2    PC3    PC4    PC5
Standard deviation     1.1077 1.0610 1.0191 0.9468 0.8440
Proportion of Variance 0.2454 0.2251 0.2077 0.1793 0.1425
Cumulative Proportion  0.2454 0.4705 0.6783 0.8575 1.0000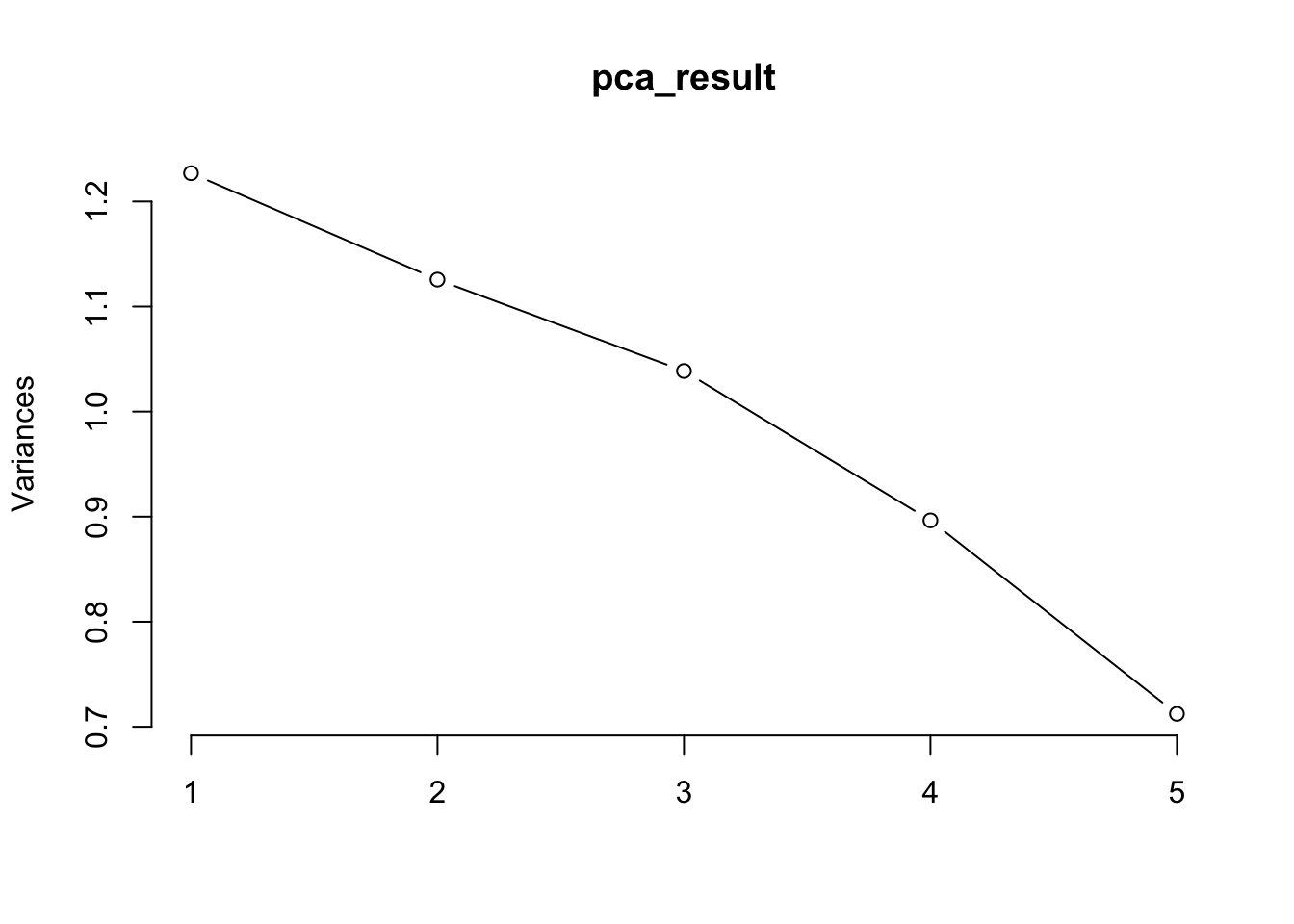

Scree-Plot zeigt die Eigenwerte der Hauptkomponenten

Biplot zeigt die Projektion der Daten und die Lasten der Variablen auf den Hauptkomponenten

13.4 Interpretation der PCA-Ergebnisse

1. Scree-Plot: Zeigt die Eigenwerte der Hauptkomponenten. Ein “Knick” im Plot deutet darauf hin, dass ab diesem Punkt weniger Varianz erklärt wird.

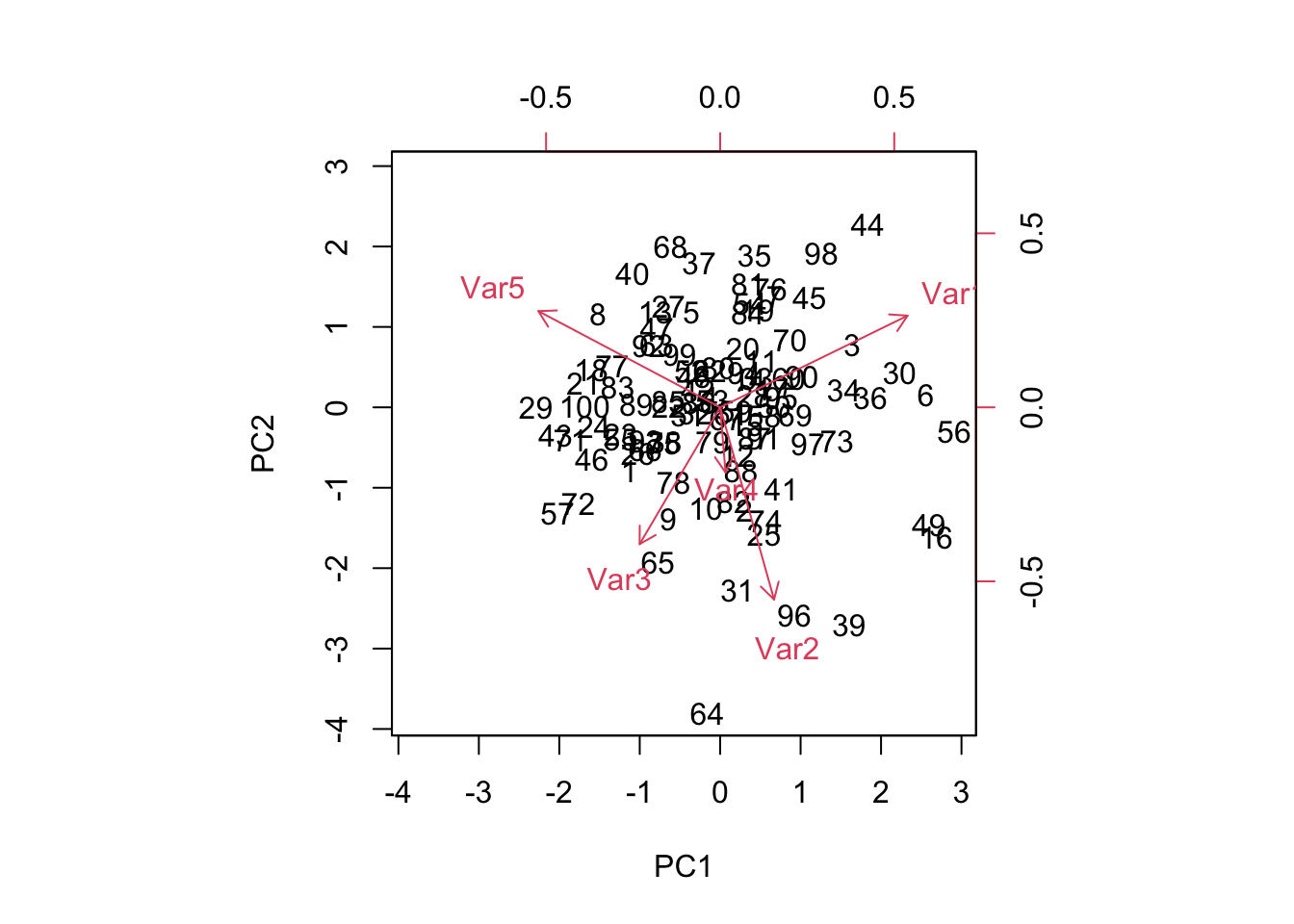
2. Biplot: Zeigt sowohl die Beobachtungen als Punkte als auch die Variablen als Vektoren. Die Länge der Vektoren zeigt die Bedeutung der Variablen, und der Winkel zwischen ihnen die Korrelation.

13.5 Fazit

Die Hauptkomponentenanalyse ist ein leistungsfähiges Werkzeug zur Reduktion von Datenkomplexität. Sie hilft, Muster in den Daten zu identifizieren und zu visualisieren, sollte jedoch mit Vorsicht interpretiert werden, da die Hauptkomponenten nicht immer eine klare inhaltliche Bedeutung haben.