8  Statistische Tests

Statistische Tests sind essenziell, um Hypothesen über Daten zu überprüfen.

8.1 Standardabweichung vs. Standardfehler

Der Standardfehler ist ein Mass für die Genauigkeit eines Schätzers. Er ist definiert als die Standardabweichung der Schätzfunktion.

\[ s_{\bar{x}} = \sqrt{\frac{s^2}{n}} \]

Wo \(s_{\bar{x}}\) der Standardfehler des Mittelwerts ist, \(s^2\) die Varianz der Stichprobe und \(n\) die Anzahl der Beobachtungen.

D.h. der Standardfehler ist gross, wenn die Varianz gross ist und/oder die Stichprobe klein ist.

Die Standardfehler sind dank dem zentralen Grenzwertsatz normalverteilt.

Beispiel

Beim Start zum Engadiner Skimarathon wird ein Bus vermisst. Bei der Suche findest du einen Parkplatz einen Bus. Du schaust in den Bus und stellt fest, dass das durchschnittliche Alter der Personen vermutlich bei ca. 80 Jahren liegt.

Die Teilnehmer am Skimarathon haben ein mittleres Alter von 40 Jahren mit einer Standardabweichung von 10 Jahren, wobei wir annehmen, dass die Alter ungefähr normalverteilt ist.

Der Standardfehler misst nun die Genauigkeit des Schätzers, also wie genau der Mittelwert der Stichprobe den Mittelwert der Population schätzt.

Im gefundenen Bus befinden sich 50 Personen mit einem durchschnittlichen Alter von 80 Jahren.

Der Standardfehler des Mittelwerts beträgt:

\[ s_{\bar{x}} = \sqrt{\frac{s^2}{n}} = \sqrt{\frac{10^2}{50}} = \sqrt{2} \approx 1.41 \text{ Jahre} \]

Die Differenz zwischen dem Mittelwert der Stichprobe und dem Mittelwert der Population beträgt 40 Jahre, und ist damit grösser als 28 Standardfehler.

Aus der Normalverteilung können wir also schliessen, dass der Bus mit 99.9% Wahrscheinlichkeit nicht die Teilnehmer des Skimarathons enthält.

8.1.1 Hypothesen

Eine Hypothese ist eine testbare Aussage über eine Population. In der Statistik gibt es zwei Hauptarten von Hypothesen:

8.1.1.1 Nullhypothese \(H_0\)

Die Nullhypothese postuliert, dass es keinen Effekt oder Unterschied gibt. Zum Beispiel könnte H₀ aussagen, dass es keinen Unterschied zwischen den Mittelwerten zweier Gruppen gibt.

8.1.1.2 Alternativhypothese \(H_A\) oder \(H_1\)

Die Alternativhypothese widerspricht der Nullhypothese und postuliert, dass es einen Effekt oder Unterschied gibt. Alternativhypothesen können einseitig (z.B. \(H_1: \mu > \mu_0\)) oder zweiseitig (z.B. \(H_1: \mu \neq \mu_0\)) sein.

8.2 Testtheorie

  1. Hypothesen aufstellen

    • Formuliere eine Nullhypothese \(H_0\) (z.B. „kein Unterschied zwischen Mittelwerten“) und eine Alternativhypothese \(H_1\) (z.B. „es gibt einen Unterschied“).

  2. Signifikanzniveau \(\alpha\) festlegen

    • Häufig \(\alpha = 0.05\). Wenn dein p-Wert kleiner ist als 0.05, lehnst du \(H_0\) ab (auf 5%-Niveau).

  3. Stichprobe erheben

    • Daten sammeln (z.B. Zufallsstichprobe) und Kennwerte (Mittelwert, Varianz, etc.) berechnen.

  4. Teststatistik berechnen

    • Beim t-Test rechnest du einen t-Wert (Teststatistik) aus. Dieser t-Wert sagt dir, wie viele „Standardfehler“ deine gemessene Differenz vom erwarteten Wert (unter \(H_0\)) entfernt ist.

    \[ t = \frac{\bar{x} - \mu_0}{s_{\bar{x}}} \]

    • \(\bar{x}\): Mittelwert deiner Stichprobe
    • \(\mu_0\): unter \(H_0\) vermuteter Populationsmittelwert (oder z.B. Differenz von 0 zwischen zwei Gruppen)
    • \(s_{\bar{x}} = \frac{s}{\sqrt{n}}\): Standardfehler des Mittelwerts, basierend auf der Stichproben-Standardabweichung \(s\) und der Stichprobengrösse \(n\)

  5. p-Wert bestimmen und Entscheidung treffen

    • Aus dem t-Wert (und den Freiheitsgraden \(\text{df} = n-1\) oder ähnlich) kannst du den p-Wert ablesen (z.B. mittels t-Verteilungstabellen oder Software). Der p-Wert gibt an, wie wahrscheinlich (oder selten) eine so grosse oder grössere Abweichung zufällig auftreten würde, wenn \(H_0\) wahr wäre.
    • Richtlinie: Ist der p-Wert kleiner als \(\alpha\) (z.B. < 0.05), lehnen wir \(H_0\) ab – das Ergebnis gilt als „statistisch signifikant“.
Beispiel

1. Hypothesen aufstellen

Schauen wir uns das Beispiel aus Kapitel 7.1.2.1.1 an. Wir haben eine Stichprobe von 5 Studierenden und ihre Prüfungsnoten (Skala 0–100).

Wir wollen testen, ob der Mittelwert der Grundgesamtheit 75 ist.

Die Null- und Alternativhypothesen lauten:

\[ H_0: \widehat{\bar{Y}} = 75 \quad \text{(kein Unterschied, Mittelwert entspricht 75)} \]

\[ H_1: \widehat{\bar{Y}} \neq 75 \quad \text{(es gibt eine Abweichung)} \]

Anmerkung zur Notation

Wir kennzeichnen Schätzungen mit einem Dach \(\widehat{X}\).

\(\widehat{\bar{Y}} = 75\) bedeutet also, dass wir den Mittelwert der Variable \(Y\) auf 75 schätzen.

Wir halten zudem fest, dass wir einen zweiseitigen Test durchführen, da wir keine Richtung der Abweichung vorgeben.

2. Signifikanzniveau \(\alpha\) festlegen

Wir entscheiden uns für ein übliches Signifikanzniveau:

\[ \alpha = 0.05 \]

Das bedeutet:

  • Falls der p-Wert kleiner als 0.05 ist, lehnen wir \(H_0\) ab und nehmen eine signifikante Abweichung an.
  • Falls der p-Wert größer als 0.05 ist, können wir \(H_0\) nicht ablehnen.

3. Stichprobe erheben

Wir übernehmen die Daten aus Tabelle 7.1 welche die Noten von 5 Studierenden enthält.

Berechnung der Kennwerte

\[ \bar{Y} = 70 \]

\[ \sigma_Y = 15.81 \]

  • Standardfehler des Mittelwerts:

    \[ \begin{aligned} s_{\bar{Y}} &= \frac{\sigma_Y}{\sqrt{n}} \\ &= \frac{15.81}{\sqrt{5}} \\ &\approx 7.07 \end{aligned} \]

4. Teststatistik berechnen

Nun berechnen wir den t-Wert mit der Formel:

\[ \begin{aligned} t &= \frac{\bar{Y} - \widehat{\bar{Y}}}{s_{\bar{Y}}} \\ &= \frac{70 - 75}{7.07} \\ &= \frac{-5}{7.07} \\ &\approx -0.71 \end{aligned} \]

  • Der t-Wert gibt an, wie viele Standardfehler der Stichprobenmittelwert von \(\widehat{\bar{Y}}\) entfernt ist.
  • Hier bedeutet \(t = -0.71\), dass unser Stichprobenmittelwert 0.71 Standardfehler unter 75 liegt.

5. p-Wert bestimmen und Entscheidung treffen

Der p-Wert wird aus der t-Verteilung mit \(df = n - 1 = 4\) Freiheitsgraden berechnet:

\[ p = 2 \times (1 - P(T \leq |t|)) \]

Wir machen das in R:

Code 
p <- pt(-0.71, df = 4) * 2 # 2 * weil zweiseitig
p
[1] 0.5169039

\[ p \approx 0.519 \]

Ergebnis:

  • \(p = 0.519 > 0.05\), also ist die Abweichung nicht signifikant.
  • Wir können \(H_0\) nicht ablehnen, d.h., die Stichprobe liefert keine ausreichenden Beweise dafür, dass wir sagen können, dass der Mittelwert der Grundgesamtheit nicht 75 ist. Wichtig: Wir haben keinen Beweis dafür, dass der Mittelwert der Grundgesamtheit 75 ist.

8.2.1 t-Test

Ein t-Test ist ein statistischer Test, der oft genutzt wird, um Mittelwerte zu vergleichen oder einen Mittelwert mit einem Referenzwert zu prüfen. Beispielsweise kannst du testen, ob das Durchschnittsgewicht einer Stichprobe signifikant von 70 kg abweicht (\(H_0: \mu = 70\)).

Voraussetzung ist, dass die Daten metrisch, ohne Ausreisser und symetrisch verteilt sind.

Der Kern des t-Tests:

  1. Du berechnest den t-Wert als \(\frac{\text{Abweichung des Mittelwerts}}{\text{Standardfehler}}\).
  2. Aus diesem t-Wert und den Freiheitsgraden (z.B. \(n-1\)) bestimmt man den p-Wert mithilfe der t-Verteilung.
  3. Ist der p-Wert kleiner als das vorab festgelegte Signifikanzniveau \(\alpha\), so lehnt man \(H_0\) ab.

Ein typisches Beispiel ist der Zweistichproben-t-Test (unabhängige Gruppen), bei dem untersucht wird, ob sich zwei Mittelwerte (z.B. Gruppe A vs. Gruppe B) signifikant unterscheiden.

8.2.1.1 t-Wert vs. p-Wert

  • Der p-Wert berechnet sich aus der t-Verteilung mit den Freiheitsgraden \(n-1\).

\[ p = 2 \times (1 - P(T \leq |t|)) \]

  • Der t-Wert ist der numerische „Abstand“ deiner beobachteten Daten (Mittelwertdifferenz) vom Wert unter \(H_0\), gemessen in Einheiten des Standardfehlers.
  • Der p-Wert ist die Wahrscheinlichkeit, einen t-Wert (oder Teststatistik) zu erhalten, der mindestens so extrem ist wie dein beobachteter, wenn \(H_0\) gilt.

Oder vereinfacht:

  • t-Wert: „Wir sind 2.5 Standardfehler vom erwarteten Wert entfernt.“
  • p-Wert: „Diese Abweichung kommt nur mit 1% Wahrscheinlichkeit zustande, wenn \(H_0\) stimmt.“

Beide Werte gehören zusammen: Ohne t-Wert weisst du nicht, wie stark die Abweichung ist; ohne p-Wert weisst du nicht, wie (un)wahrscheinlich diese Abweichung unter der Nullhypothese wäre.

8.2.2 Fehlerarten

Testentscheidung \(H_0\) nicht ablehnen \(H_0\) ablehnen
\(H_0\) wahr Richtige Entscheidung Fehler 1. Art
\(H_0\) falsch Fehler 2. Art Richtige Entscheidung
  • Fehler 1. Art (Alpha-Fehler): Wir lehnen \(H_0\) ab, obwohl \(H_0\) wahr ist.
  • Fehler 2. Art (Beta-Fehler): Wir nehmen \(H_0\) an, obwohl \(H_0\) falsch ist.
  • Es gibt keine Testverfahren, die beide Fehlerarten gleichzeitig minimieren können.
  • Das Signifikanzniveau \(\alpha\) ist die Wahrscheinlichkeit für einen Fehler 1. Art.
  • Der Fehler 2. Art ist in der Regel weniger gravierend.

8.2.3 Mittwelwerte Testen

  • Mittelwert \(\mu\) und Standardabweichung \(\sigma\) aus \(X_{\text{Mittel}}\) und \(s_x\) schätzen.
  • Das führt bei kleinen Stichproben zu grossen Standardfehlern.
  • es ist unwahrscheinlich, dass die Stichprobe exakt das Mittel der Grundgesamtheit trifft.
  • Dadurch wird die Verteilung der Teststatistik \(t\) breiter.

T-Verteilung

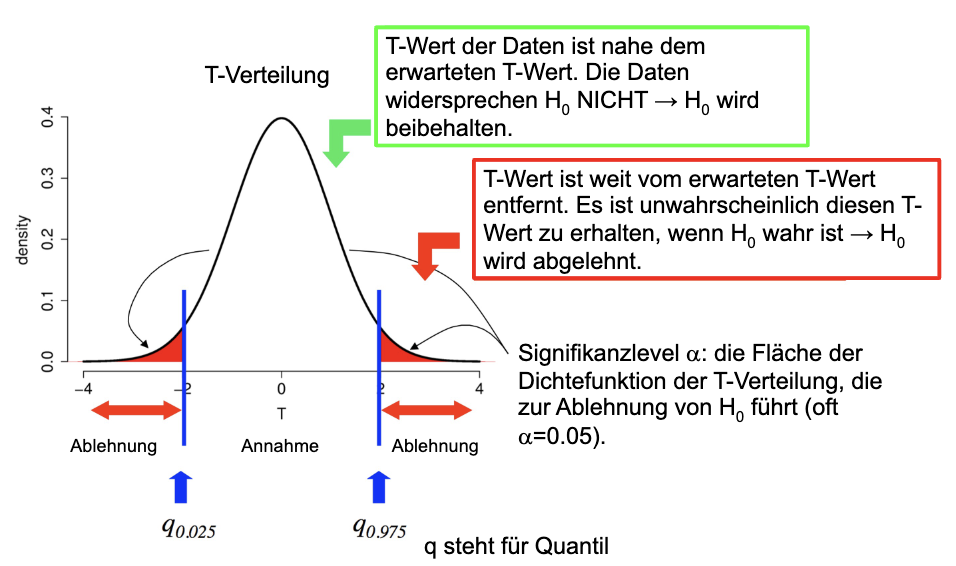
Dieser Test ist ein zweiseitiger Test mit \(\alpha = 0.05\). Das führt dazu, dass wir die Quantile so verteilen, dass “unten” 2.5% der Fläche und “oben” 2.5% der Fläche liegen.

Bei einem einseitigen Test wäre \(\alpha = 0.05\) und wir würden die Quantile so verteilen, dass “unten” 5% der Fläche und “oben” 95% der Fläche liegen.

8.3 Konfidenzintervalle

  • Masszahl für die Unsicherheit der Parameterschätzung
  • Konfidenzintervalle sind Intervalle, die den wahren Wert einer Grundgesamtheit mit einer bestimmten Wahrscheinlichkeit schätzen.
  • Eng verknüpft mit dem Signifikanzlevel \(\alpha\)

Allgemeine Formel:

Ein \((1 - \alpha)\)-Konfidenzintervall für den Mittelwert wird berechnet mit:

\[ \operatorname{CI}_{(1-\alpha)} = \bar{x} \pm t_{\alpha/2, df} \cdot s_{\bar{x}} \]

wobei:

  • \(\bar{x}\) = Mittelwert der Stichprobe
  • \(t_{\alpha/2, df}\) = kritischer t-Wert aus der t-Verteilung mit \(df = n - 1\) Freiheitsgraden
  • \(s_{\bar{x}}\) = Standardfehler des Mittelwerts
Beispiel

Nachdem wir in unserem t-Test festgestellt haben, dass wir die Nullhypothese \(H_0: \mu = 75\) nicht ablehnen können, wollen wir nun ein 95%-Konfidenzintervall (CI) für den Mittelwert der Grundgesamtheit bestimmen. Das Konfidenzintervall gibt uns einen Bereich, in dem der wahre Mittelwert mit 95% Wahrscheinlichkeit liegt.

1. Berechnungen für unser Beispiel aus Kapitel 7.1.2.1.1

Gegeben:

Wert Berechnung Ergebnis
Stichprobe \(Y = \{70, 80, 50, 90, 60\}\)
Stichprobenmittelwert \(\bar{Y}\) \(\frac{70+80+50+90+60}{5}\) 70.00
Stichprobenstandardabweichung \(s\) \(\sqrt{\frac{\sum (Y_i - \bar{Y})^2}{n-1}}\) 15.81
Standardfehler \(s_{\bar{Y}}\) \(\frac{s}{\sqrt{n}}\) 7.07
Freiheitsgrade \(df\) \(n-1 = 4\) 4

2. Kritischen t-Wert für \(\alpha = 0.05\) bestimmen

Da wir ein 95%-Konfidenzintervall berechnen, setzen wir:

\[ \alpha = 0.05 \quad \Rightarrow \quad t_{\alpha/2, df=4} \]

Den kritischen t-Wert können wir in R mit qt() berechnen:

alpha <- 0.05
df <- 4
t_crit <- qt(1 - alpha/2, df)
t_crit
[1] 2.776445

Ergebnis:

\[ t_{\alpha/2,4} = 2.776 \]

3. Konfidenzintervall berechnen

Nun setzen wir alles in die Formel ein:

x_bar <- 70    # Mittelwert der Stichprobe
s_x_bar <- 7.07  # Standardfehler des Mittelwerts
ci_lower <- x_bar - t_crit * s_x_bar
ci_upper <- x_bar + t_crit * s_x_bar
c(ci_lower, ci_upper)
[1] 50.37053 89.62947

\[ CI_{95\%} = [50.37, 89.63] \]

4. Interpretation

  • Wir sind 95% sicher, dass der wahre Mittelwert der Grundgesamtheit zwischen 50.37 und 89.63 liegt.
  • Da 75 innerhalb dieses Intervalls liegt, gibt es keine signifikante Abweichung von 75 – das bestätigt unser vorheriges Testergebnis.
  • Das breite Intervall zeigt eine hohe Streuung oder eine kleine Stichprobe, was bedeutet, dass unsere Schätzung noch unsicher ist.

Daumenregel:

\[ \text{Konfidenzintervall} = \text{Stichprobenergebnis} \pm 2 \cdot \text{Standardfehler} \]

8.4 Überprüfung auf Normalverteilung

Wir stellen auch hier entsprechende Hypothesen auf.

\[ \begin{aligned} H_0: &\text{Daten sind normalverteilt} \\ H_A: &\text{Daten sind nicht normalverteilt} \end{aligned} \]

Dass wir hier mit der \(H_0\) die Normalverteilung testen, ist nicht intuitiv. Aber wir testen hier nicht, ob die Daten normalverteilt sind, sondern ob sie nicht normalverteilt sind. Wenn wir das Gegenteil beweisen wollen, müssen wir das Gegenteil widerlegen.

Eine Normalverteilung kann man nicht beweisen, sondern nur widerlegen.

Test Vorteile Nachteile
\(\chi^2\)-Test
  • geeignet für beliebig skalierte Variablen

  • Gruppierung der Beobachtungen notwendig

  • ungeeignet für kleine Stichproben

  • quadratische Testgrösse, d.h. sensibel auf Ausreisser
Kolmogorov-Smirnov-Test

  • geeignet für kleine Stichproben

  • wie Chi-Quadrat auch zum Vergleich anderer Verteilungen geeignet

  • nicht-parametrischer Test, d.h. nicht sensibel auf Ausreisser
  • geringe Teststärke im Vergleich zu den folgenden Tests
Cramér-von-Mises-Test
  • höhere Güte als KS-Test
  • quadratische Testgrösse
Lilliefors-Test

  • bessere Trennschärfe als KS-Test

  • nicht-parametrischer Test
  • nur zum Test auf Normalverteilung
Anderson-Darling-Test
  • sehr hohe Güte bei Test auf Normalverteilung

  • keine kategorialen Daten

  • quadratische Testgrösse
Shapiro-Wilk-Test
  • Test mit höchster Güte

  • ausschliesslich Test auf Normalverteilung

  • manuell schlecht durchführbar

  • sensibel auf Ausreisser und viele identische Werte

8.4.1 Überprüfung auf Normalverteilung in R

# Daten generieren
set.seed(123)
normal_data <- rnorm(500)        # 500 normalverteilte Zufallszahlen
non_normal_data <- normal_data^2 # quadrierte Zufallszahlen (nicht normalverteilt)

# Shapiro-Wilk-Test für beide Datensätze
shapiro_result_normal <- shapiro.test(normal_data)
shapiro_result_non_normal <- shapiro.test(non_normal_data)

# Shapiro-Wilk-Test für normal_data:
cat("W-Teststatistik:", round(shapiro_result_normal$statistic, 4), "\n")
W-Teststatistik: 0.9981 
cat("p-Wert:", round(shapiro_result_normal$p.value, 4), "\n")
p-Wert: 0.8639 
# Shapiro-Wilk-Test für non_normal_data:
cat("W-Teststatistik:", round(shapiro_result_non_normal$statistic, 4), "\n")
W-Teststatistik: 0.708 
cat("p-Wert:", round(shapiro_result_non_normal$p.value, 4), "\n")
p-Wert: 0
Code 
if (shapiro_result_normal$p.value > 0.05) {
  cat("Die Nullhypothese der Normalverteilung kann nicht verworfen werden. \n`normal_data` ist normalverteilt.\n\n")
} else {
  cat("Die Nullhypothese der Normalverteilung wird verworfen. \n`normal_data` ist **nicht** normalverteilt.\n\n")
}

Die Nullhypothese der Normalverteilung kann nicht verworfen werden. normal_data ist normalverteilt.

Code 
if (shapiro_result_non_normal$p.value > 0.05) {
  cat("Die Nullhypothese der Normalverteilung kann nicht verworfen werden. \n`non_normal_data` ist normalverteilt.\n\n")
} else {
  cat("Die Nullhypothese der Normalverteilung wird verworfen. \n`non_normal_data` ist **nicht** normalverteilt.\n\n")
}

Die Nullhypothese der Normalverteilung wird verworfen. non_normal_data ist nicht normalverteilt.

Code 
# Layout für nebeneinanderstehende Plots definieren
par(mfrow = c(2, 2), mar = c(4, 4, 2, 1))

# Histogramm
hist(normal_data, 
     main = "Histogramm (Normalverteilung)", 
     xlab = "Werte", 
     col = "lightblue", 
     border = "white")
hist(non_normal_data, 
     main = "Histogramm (Nicht Normalverteilt)", 
     xlab = "Werte", 
     col = "lightcoral", 
     border = "white")

# Dichtefunktion
plot(density(normal_data), 
     main = "Dichtefunktion (Normalverteilung)", 
     xlab = "Werte", 
     col = "darkblue", 
     lwd = 2)
plot(density(non_normal_data), 
     main = "Dichtefunktion (Nicht Normalverteilt)", 
     xlab = "Werte", 
     col = "darkred", 
     lwd = 2)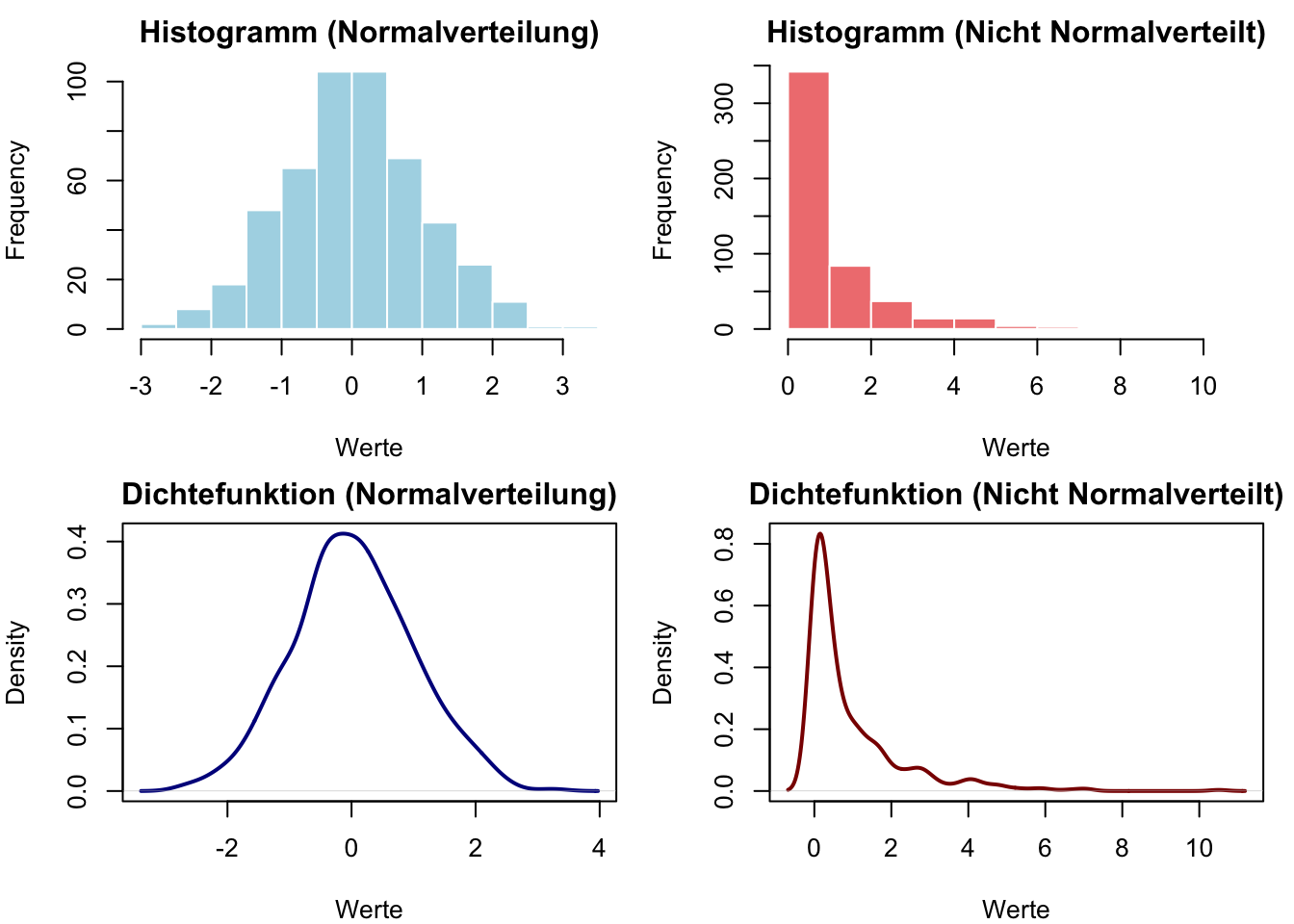

Visualisierung der Normalverteilung
Code 
# Boxplot
boxplot(normal_data, 
        main = "Boxplot (Normalverteilung)", 
        col = "lightgreen", 
        horizontal = TRUE)
boxplot(non_normal_data, 
        main = "Boxplot (Nicht Normalverteilt)", 
        col = "lightpink", 
        horizontal = TRUE)

# QQ-Plot
qqnorm(normal_data, 
       main = "QQ-Plot (Normalverteilung)")
qqline(normal_data, col = "red", lwd = 2)

qqnorm(non_normal_data, 
       main = "QQ-Plot (Nicht Normalverteilt)")
qqline(non_normal_data, col = "red", lwd = 2)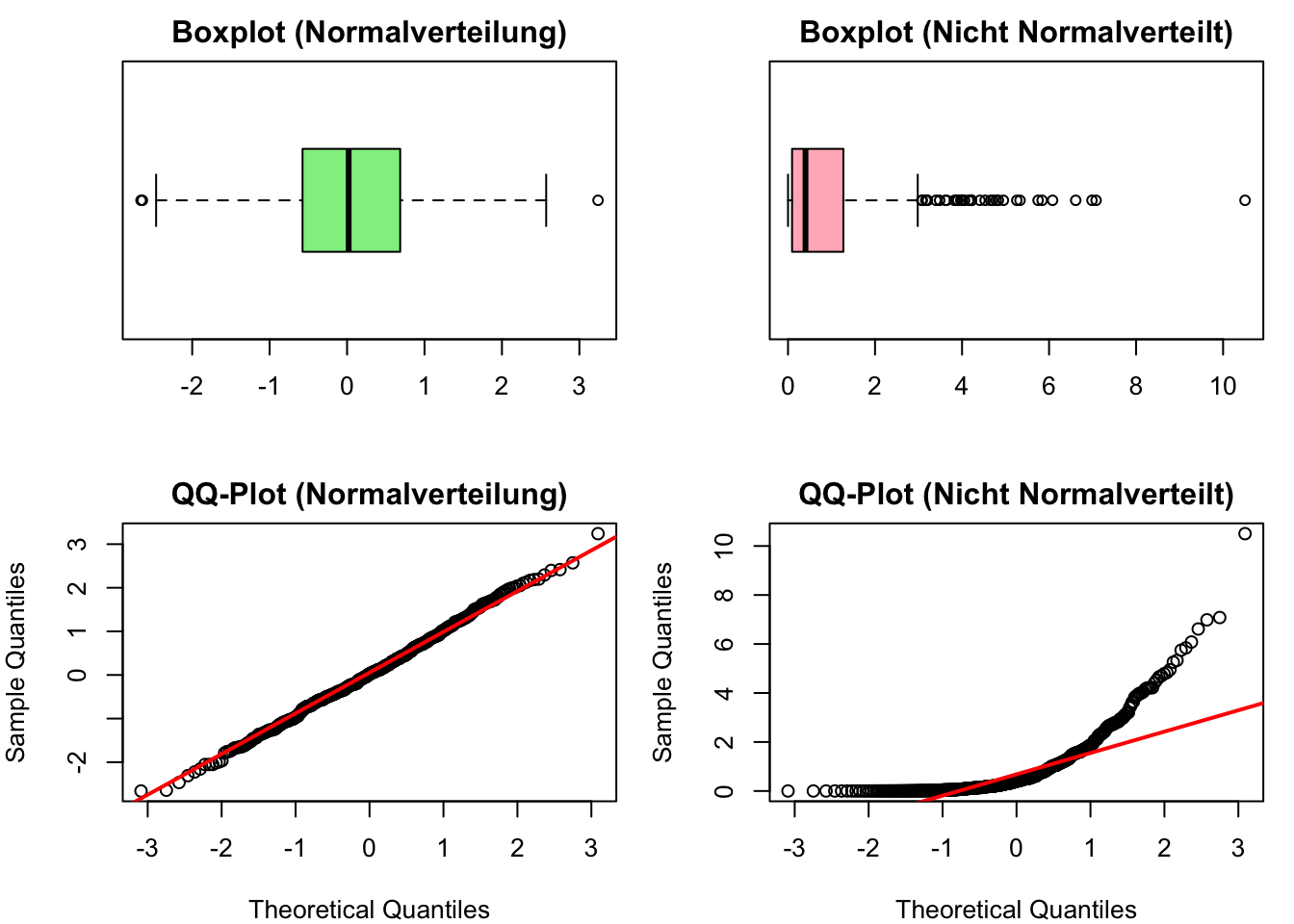

Visualisierung der Normalverteilung
Code 
# Layout zurücksetzen
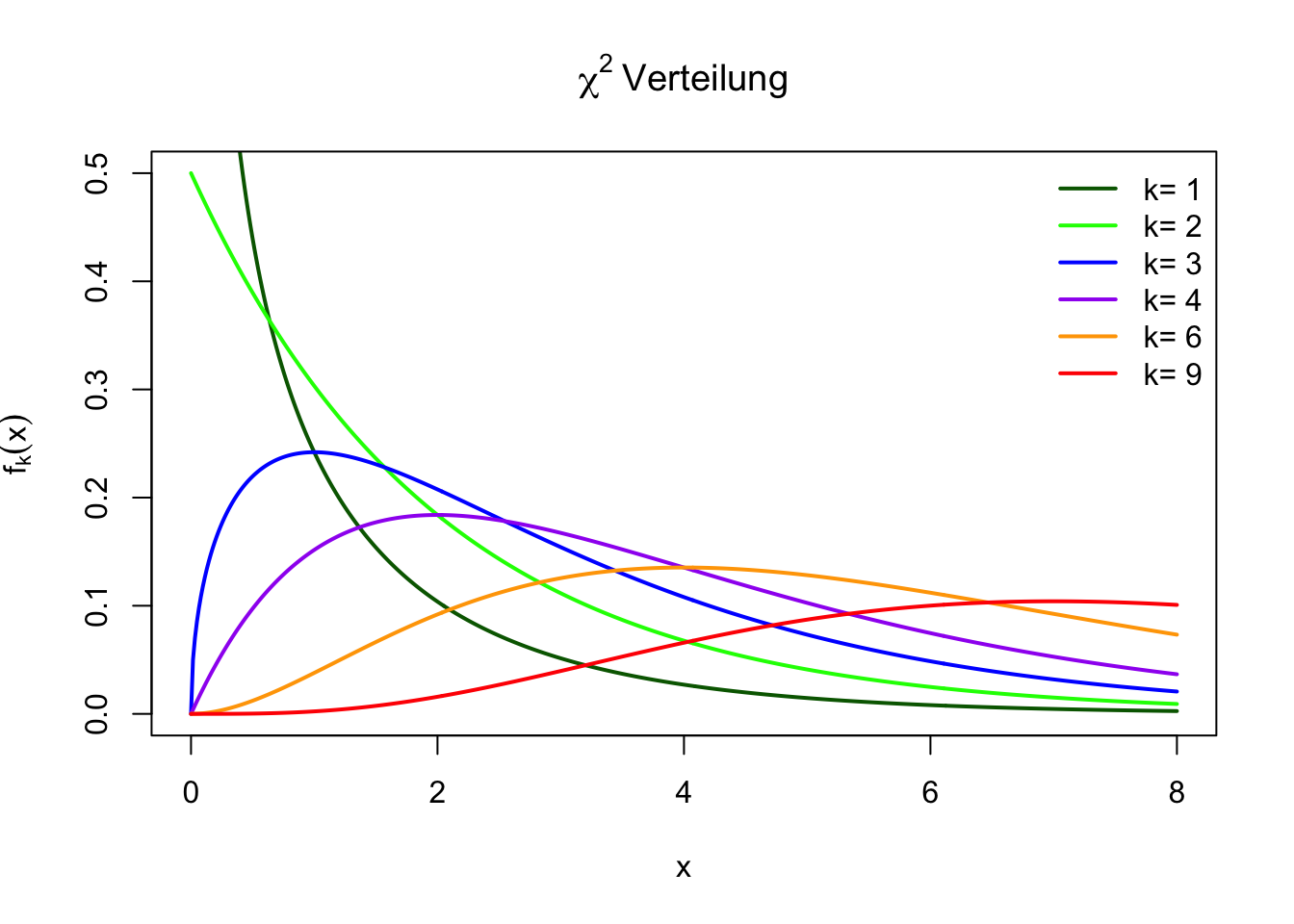
par(mfrow = c(1, 1))

8.4.2 \(\chi^2\)-Test

  • Summe der quadrierten Abweichungen:

\[ \chi^2 = \sum_{i=1}^{k} \frac{(N_i - n_i)^2}{n_i} \]

  • \(N_i\): beobachtete Häufigkeit in der Klasse \(i\)
  • \(n_i\): erwartete Häufigkeit in der Klasse \(i\)
  • \(k\): Anzahl der Klassen

8.4.2.1 \(\chi^2\)-Verteilung

  • stetige Wahrscheinlichkeitsverteilung mit der Anzahl Freiheitsgrade \(k\) als einzigem Parameter
  • Verteilung der Summe der Quadrate von \(k\) unabhängigen und standardnormalverteilten Zufallsvariablen.
Code 
# Chi-Quadrat-Verteilung plotten
x <- seq(0, 8, length.out = 500)
df_values <- c(1, 2, 3, 4, 6, 9)

# Farben definieren
colors <- c("darkgreen", "green", "blue", "purple", "orange", "red")

# Plot erstellen
plot(x, dchisq(x, df = 1), type = "l", lwd = 2, col = colors[1], 
     ylim = c(0, 0.5), xlab = "x", ylab = expression(f[k](x)), 
     main = expression(chi^2~"Verteilung"))

# Weitere Linien hinzufügen
for (i in 2:length(df_values)) {
  lines(x, dchisq(x, df = df_values[i]), col = colors[i], lwd = 2)
}

# Legende hinzufügen
legend("topright", legend = paste("k=", df_values), 
       col = colors, lwd = 2, bty = "n")

Chi-Quadrat-Verteilung

8.5 Testauswahl

Testauswahl Quelle: Methodenberatung UZH